
The infrared spectrum of a molecule is a result of transitions between two different vibrational energy levels.
Vibrational motions of a molecule resemble the motions observed for 2 balls attached to a spring as shown in figure 1 .
Consider:

Potential energy Ep =½k(d1 +d2 )2
Where k is the force constant of the spring, d1 & d2 are the displacements of the spring.
Frequency of vibrations
![]()
Because in a molecular situation the frequency of vibration is a function of the masses of the atoms and the strength of the bond (force constant k), the quantity given as: m1m2 is called the reduced mass,![]()
It is important that we are viewing the vibrations of the molecule from a stationary point of view, because a stationary point does not change its position with time. It is therefore important to use reduced mass when we are dealing with mathematical calculations in quantum mechanics because time is not involved in the formulations.
However, the chemical bond differs from the simple harmonic motions of this system because the vibrational energy of the bond is quantised and only certain energy levels are allowed.
E vibrational =(v+½)h
v is the vibrational quantum number, h is Plank's constant and ? frequency of the bond. See figure 1 .
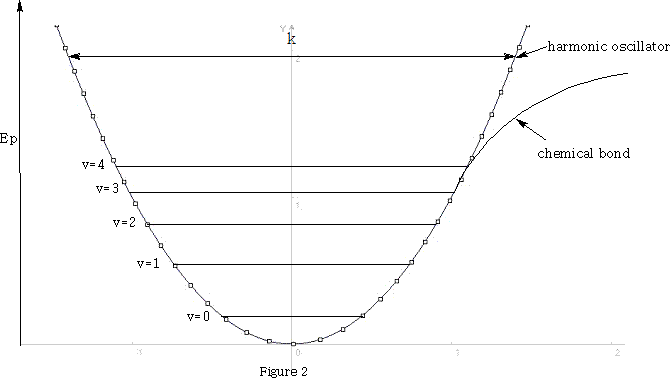
At room temperature, where molecules are in there lowest vibrational state, the harmonic oscillator model is a good approximation of the chemical bond. Transitions from the ground state v=0 to v=1 absorb light in the IR range to give intense fundamental spectral bands. Vibrations from v=0 to v=2 absorb light and give rise to weak overtones. Hence hνlight =hνvibration when transitions are v=0 to v=1.
We have only looked at systems with two atoms, how does this affect the IR absorption, because polyatomic molecules will exhibit more than one fundamental vibrational absorption band. The number of bands is related to the degrees of freedom that the molecule has. The degrees of freedom are equal to the sum of the coordinates necessary to locate all the atoms of the molecule in space. Atoms have three degrees of freedom, all of which are translational(X, Y, Z) when atoms combine too form molecules; no degrees of freedom are lost. Hence the total number of degrees of freedom will be 3n where n is the number of atoms in the molecule. The 3n degrees of freedom will be made up of rotational, vibrational and translational degrees of freedom.
Hence, 3n degrees of freedom= translational + rotational + vibrational
For a molecule with two atoms it will have 3(2)=6 degrees of freedom. Three will be translational, two will be rotational!? If we look at figure 3 we can see that only rotation about y and z will result in a change of position of the atoms, x does not.
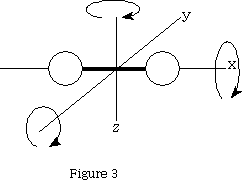
That leaves 3n-5 vibrational degrees of freedom=1 when n=2.
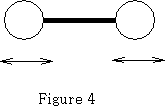
The molecule vibrates as shown in figure 4.
Consider now a three atom molecule like CO2. It is linear.
![]()
Total degrees of freedom = 3n = 9
Translational = 3
Rotation = 2 same reason as for a two atom molecule.
Vibrational = 9 5 = 4.
Four vibrational bands!
What will be these vibrations?
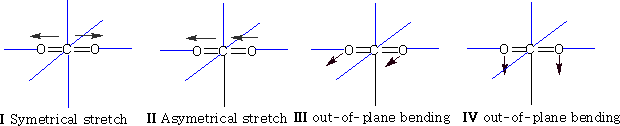

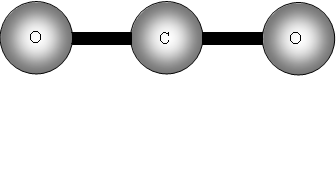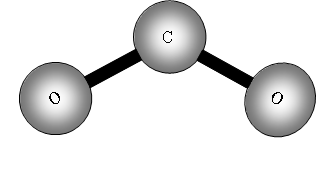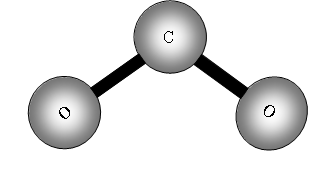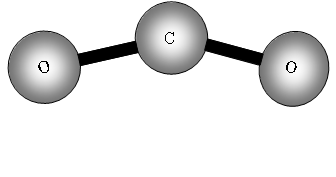
The two out of plane bending will be equivalent as it is only the direction in which they are bending, they are said to be degenerate.
An infrared absorption will be observed for each vibrational degree of freedom provided:
• A change in the dipole moment of the molecule occurs during vibration
• The band does not coincide in frequency with some other fundamental vibration.
• The absorption falls within the IR spectrum
• The intensity of the absorption is strong enough to be detected.
Additional bands may occur due to the overtones mentioned earlier and combination tones.
How many bands will we get with CO2? The answer is two! Why? The first symmetric stretch I does not have a dipole change, so that one is inactive.
II has a dipole change that is the first peak; III and IV are equivalent (degenerate) so only produce one band, which is the second peak.

We can go further now because a three atom molecule can be non-linear: e.g. Water
![]()
This time because the molecule is not linear the number of degrees of freedom for rotation is 3, therefore vibrational freedoms = 9 - 6 = 3.
What are they?
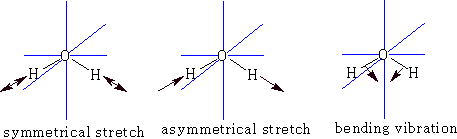
Each of the vibrations has a dipole change so there will be three peaks possible.
Measurement of IR
1 Double beam spectrometer
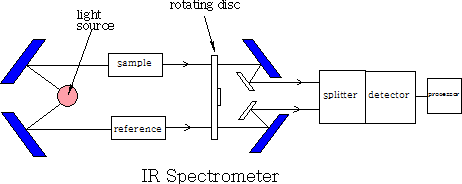
A beam of light is split into two, one beam is passed through the sample and one through the reference, each beam then passes through a rotating disc which passes the two beams alternately into the splitter, they are then detected and compared and then sent to be recorded. The recorder plots the transmittance (the percentage of radiation that passes through the sample) against the wavenumber (1/wavelength ). The instrument does not use glass or quartz because both absorb IR radiation. All mirrors and prisms are made from large NaCl crystals.
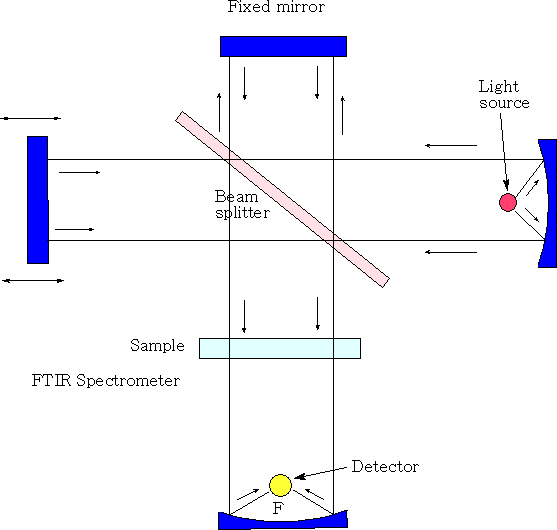
Michelson interferometer
In the Michelson interferometer a parallel, polychromatic beam of radiation from a light source is directed to a beam splitter, made from an infrared transparent material, such as KBr. The beam splitter reflects approximately half of the light to a mirror, known as the fixed mirror, which in turn reflects the light back to the beam splitter. The rest of the light passes through to a mirror, moving continuously, at a known velocity, back and forth along the direction of the incoming light and this is known as the moving mirror. Upon reflection from the moving mirror, radiation is then directed back to the beam splitter. At the beam splitter some of the light that has been reflected from the fixed mirror combines with light reflected from the moving mirror and is directed towards the sample. After passing through the sample the radiation is focused onto the detector. The detectors are sufficiently fast to cope with time domain signal changes from the modulation in the interferometer. As the distance of the moving mirror from the beam splitter changes, different wavelengths of radiation are in-phase and out-of-phase at a frequency that is dependent both upon the rate at which the mirror moves and the frequency of radiation.
Typical Infrared Absorption Frequencies