When nuclei spin about their axis they create a nuclear spin angular momentum, this momentum is quantised and is designated by the nuclear spin quantum number (s.q.n) I . The nuclear spin number may have a value of 0, ½, 1, 1½, etc. depending on the nucleus. Only certain nuclei possess a spin angular momentum. If the mass number ( A ) is odd, then the s.q.n I is a half integer (n+½, where n is a whole no. or zero). If the mass number and the atomic number ( Z ) are both even, the s.q.n I is zero. If the mass number is even and the atomic number is odd, the s.q.n I is an integer (1, 2, 3 etc.). Only those nuclei with an I value greater than zero have a spin angular momentum.
When placed in a magnetic field, nuclei with an angular momentum will give 2 I +1 orientations. Each orientation relates to the energy state for the nucleus.
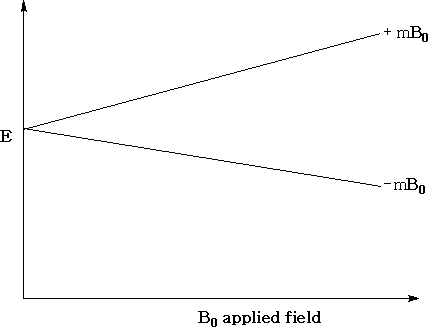
For a proton (1H1 ), the number of orientations is 2(½) + 1= 2. The energy of each orientation corresponds to ±µHB0 where µH is the magnetic moment of the proton and B0 , is the strength of the applied field.

The above diagram shows the variation in the energy levels as a function of the strength of the applied field. You can see that when the applied field is zero the energy levels are the same.
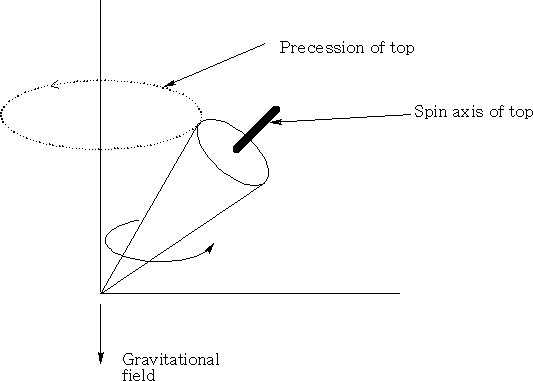
Consider a top when it spins; if the spin axis is not parallel to the gravitation field it will precess, that is rotate in a circle perpendicular to the gravitational field. (See diagram above )
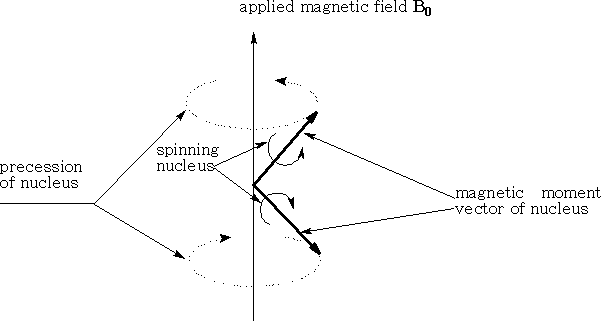
A hydrogen atom which has a spin ½ is similar to the spinning top; it will precess about a point. The magnetic moment of the nucleus will line up or oppose the applied magnetic field. The magnetic moment cannot line up exactly with the field so it will precess about it. The stronger the field the faster will be the precession. (See diagram above)
The hydrogen nucleus as we have seen can exist in two states, either lined with the applied field or against it. The transition of the Hydrogen nucleus from one state to the other requires an amount of energy equal to 2µHB0 . This energy can be supplied by electromagnetic radiation applied in a specific way i.e. the radiations magnetic vector is oscillating in a plane perpendicular to the applied field.
The nuclei will reach resonance when the oscillating magnetic field is equal to the precessing frequency of the magnetic moment of the nucleus. Energy can then be transferred from the electromagnetic radiation to the hydrogen nucleus. At resonance the proton will flip from one state to another.
Hence:
ΔE = 2µHB0
Since ΔE = hν
Therefore: hν = 2µH B0
ν = 2µHB0 / h
ν = µHB0 / h I where I is the spin quantum number.
The equation is usually expressed as ν= γB0 /2π where γ is the gyromagnetic ratio of the nucleus.
The precessional angular velocity ω0 is equal to the gyromagnetic ratio and the strength of the applied field, hence,ω0 = γB0 , therefore, ω0 = 2πν
To measure the transition of a proton from one spin to another, a fixed electromagnetic radiation frequency is imposed and the magnetic field varied until the resonance situation is reached. A fixed oscillator of 60 MHz will require a field of 1.4 tesla (T). A fixed oscillator of 900MHz will require a field of 21T. Large fields are best to get a measurable separation of energy levels. Each proton will be affected differently by the applied field depending on the chemical environment of the proton.
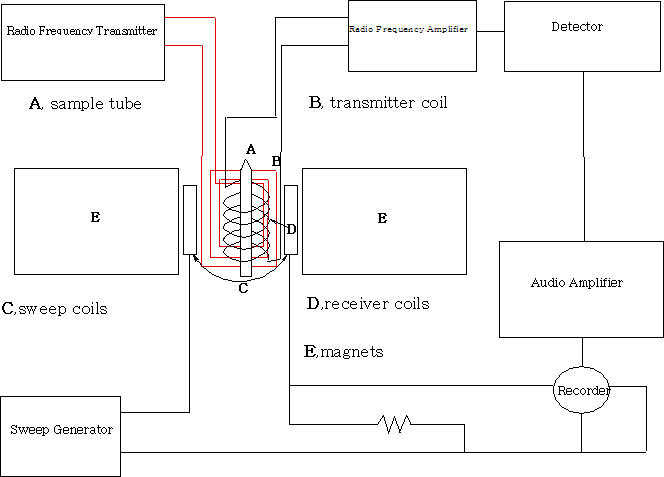
Measuring NMR spectra
All NMR machines above 100MHz require helium cooled superconducting magnets and operate in an FT mode. The important features of this are that they have frequency-field stability and have field homogeneity.
The sample (usually in a deuterated solvent) is placed in a 5mm tube and into the probe which consists of the transmitter, receiver coils and a spinner. The spinner spins the sample at high speed about its vertical axis in order to average out any inhomogeneities. In the non-superconducting magnet system the sample spins perpendicular to the z axis of the magnet. The diagram is that of a non-superconducting magnet system. The magnetic field is varied and the changes in the sample recorded.